一、为什么SSA不能证明三角形全等
1、在学习三角形全等的时候,我们通常使用SSS、SAS、ASA、AAS等方法来判断两个三角形是否全等。然而,使用SSA(两条边和其夹角)来证明三角形全等时,无法保证三角形一定全等。这是因为在某些情况下,两个三角形的SSA条件相等但未必是全等的。
2、具体来说,当两个三角形的其中一条边的长度小于或等于另一条边的长度时,就可能存在无法确定三角形是否全等的情况。
3、因此,在判断三角形是否全等时,需要注意不同条件的适用范围,以免出现错误的结论。
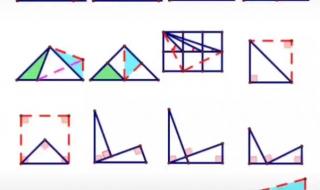
二、为什么边边角不能证明三角形全等
这个角必须是这两条边的夹角才能证明三角形全等,如果不是这两条边的夹角就不能证明全等.比如直角三角形,都有一个90度角,它的三条边既可以是3,4,5,也可以是3,5,根号下34!它们就满足“边边角”,但是很明显它们不全等!
三、三角形全等和三角形相似的区别
全等三角形大小、形状相等相等,对应边相等,对应角相等与相似三角形形状相同,但大小可能不同,对应边成比例,对应角相等;相似三角形含全等三角形。
四、三角形全等定理及其证明
1、三组对应边分别相等的两个三角形全等(简称SSS或“边边边”),这一条也说明了三角形具有稳定性的原因.2、有两边及其夹角对应相等的两个三角形全等(SAS或“边角边”)
.3、有两角及其夹边对应相等的两个三角形全等(ASA或“角边角”)
.4、有两角及其一角的对边对应相等的两个三角形全等(AAS或“角角边”
) 5、直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(HL或“斜边,直角边”) 所以,SSS,SAS,ASA,AAS,HL均为判定三角形全等的定理.
五、不同平面还能用全等三角形吗
当然可以。三点确定一个平面,一个三角形就是一个平面,三角形全等定夂就有翻转,平移,翻转和平移就代表不同平面,既然两个三角形是全等三角形,不管是翻转还是平移(平移可在同一平面,可在上下不同平面),它们还是全等三角形,当然在不同平面还能用全等三角形的特性解决问题



本文《为什么SSA不能证明三角形全等 全等三角形难题》希望能帮助到你!